How to Do Lcs When You Dont Know How Many Strings Are in a File C++
We have discussed Overlapping Subproblems and Optimal Substructure properties in Set 1 and Set 2 respectively. We also discussed 1 example trouble in Gear up 3. Let united states of america discuss Longest Common Subsequence (LCS) problem equally one more than example problem that can be solved using Dynamic Programming.
LCS Trouble Statement: Given ii sequences, find the length of longest subsequence present in both of them. A subsequence is a sequence that appears in the same relative gild, only not necessarily contiguous. For example, "abc", "abg", "bdf", "aeg", '"acefg", .. etc are subsequences of "abcdefg".
In order to find out the complexity of fauna strength approach, we need to commencement know the number of possible different subsequences of a string with length n, i.e., discover the number of subsequences with lengths ranging from 1,2,..n-ane. Remember from theory of permutation and combination that number of combinations with one element are northC1. Number of combinations with 2 elements are northC2 and so forth and so on. We know that nC0 + northC1 + nC2 + … northwardCnorth = twodue north. So a string of length due north has iinorth-1 different possible subsequences since we do not consider the subsequence with length 0. This implies that the fourth dimension complexity of the brute force approach volition be O(due north * twon). Notation that it takes O(due north) time to cheque if a subsequence is common to both the strings. This time complexity can be improved using dynamic programming.
It is a archetype information science problem, the basis of diff (a file comparing plan that outputs the differences between two files), and has applications in bioinformatics.
Examples:
LCS for input Sequences "ABCDGH" and "AEDFHR" is "ADH" of length 3.
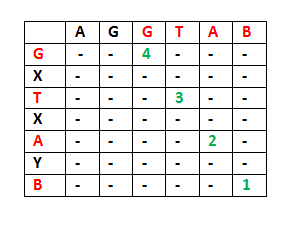
LCS for input Sequences "AGGTAB" and "GXTXAYB" is "GTAB" of length 4.
Recommended: Delight endeavor your approach on {IDE} start, before moving on to the solution.
The naive solution for this problem is to generate all subsequences of both given sequences and find the longest matching subsequence. This solution is exponential in term of time complexity. Permit us run into how this problem possesses both important properties of a Dynamic Programming (DP) Trouble.
one) Optimal Substructure:
Permit the input sequences be Ten[0..1000-1] and Y[0..north-one] of lengths m and due north respectively. And allow L(X[0..thou-1], Y[0..n-1]) be the length of LCS of the two sequences X and Y. Post-obit is the recursive definition of L(X[0..1000-1], Y[0..due north-1]).
If last characters of both sequences lucifer (or X[m-i] == Y[n-1]) so
L(10[0..thousand-one], Y[0..n-ane]) = ane + Fifty(X[0..chiliad-two], Y[0..northward-ii])
If concluding characters of both sequences exercise not match (or X[m-1] != Y[n-1]) then
50(X[0..m-1], Y[0..n-1]) = MAX ( Fifty(X[0..one thousand-2], Y[0..n-one]), L(10[0..m-1], Y[0..n-2]) )
Examples:
ane) Consider the input strings "AGGTAB" and "GXTXAYB". Last characters friction match for the strings. So length of LCS tin can exist written as:
Fifty("AGGTAB", "GXTXAYB") = ane + L("AGGTA", "GXTXAY")
2) Consider the input strings "ABCDGH" and "AEDFHR. Last characters do not lucifer for the strings. So length of LCS can be written every bit:
L("ABCDGH", "AEDFHR") = MAX ( L("ABCDG", "AEDFHR"), L("ABCDGH", "AEDFH") )
So the LCS trouble has optimal substructure belongings equally the principal problem can exist solved using solutions to subproblems.
ii) Overlapping Subproblems:
Following is unproblematic recursive implementation of the LCS problem. The implementation just follows the recursive construction mentioned higher up.
C++
#include <bits/stdc++.h>
using namespace std;
int lcs( char *X, char *Y, int one thousand, int n )
{
if (m == 0 || due north == 0)
return 0;
if (X[thousand-1] == Y[north-ane])
return 1 + lcs(Ten, Y, m-1, n-one);
else
return max(lcs(X, Y, chiliad, n-1), lcs(X, Y, grand-1, n));
}
int principal()
{
char 10[] = "AGGTAB" ;
char Y[] = "GXTXAYB" ;
int chiliad = strlen (X);
int n = strlen (Y);
cout<< "Length of LCS is " << lcs( X, Y, thousand, n ) ;
return 0;
}
C
#include<$.25/stdc++.h>
int max( int a, int b);
int lcs( char *X, char *Y, int thousand, int n )
{
if (m == 0 || north == 0)
return 0;
if (10[yard-1] == Y[due north-i])
return ane + lcs(X, Y, m-1, n-ane);
else
return max(lcs(Ten, Y, m, n-1), lcs(X, Y, chiliad-1, north));
}
int max( int a, int b)
{
return (a > b)? a : b;
}
int main()
{
char 10[] = "AGGTAB" ;
char Y[] = "GXTXAYB" ;
int thousand = strlen (X);
int n = strlen (Y);
printf ( "Length of LCS is %d" , lcs( 10, Y, m, n ) );
return 0;
}
Java
public form LongestCommonSubsequence
{
int lcs( char [] X, char [] Y, int m, int n )
{
if (chiliad == 0 || n == 0 )
return 0 ;
if (10[k- 1 ] == Y[n- 1 ])
return 1 + lcs(X, Y, m- one , due north- 1 );
else
render max(lcs(X, Y, m, n- ane ), lcs(X, Y, 1000- 1 , n));
}
int max( int a, int b)
{
return (a > b)? a : b;
}
public static void chief(String[] args)
{
LongestCommonSubsequence lcs = new LongestCommonSubsequence();
String s1 = "AGGTAB" ;
String s2 = "GXTXAYB" ;
char [] Ten=s1.toCharArray();
char [] Y=s2.toCharArray();
int m = X.length;
int n = Y.length;
Arrangement.out.println( "Length of LCS is" + " " +
lcs.lcs( X, Y, g, n ) );
}
}
Python3
def lcs(X, Y, g, n):
if thousand = = 0 or n = = 0 :
render 0
elif X[g - 1 ] = = Y[northward - 1 ]:
return 1 + lcs(Ten, Y, m - ane , n - one );
else :
return max (lcs(10, Y, m, n - one ), lcs(X, Y, m - 1 , n));
X = "AGGTAB"
Y = "GXTXAYB"
print ( "Length of LCS is " , lcs(X , Y, len (X), len (Y)) )
C#
using System;
class GFG
{
static int lcs( char [] 10, char [] Y, int m, int n )
{
if (yard == 0 || n == 0)
return 0;
if (Ten[thou - one] == Y[n - 1])
return 1 + lcs(Ten, Y, m - 1, north - 1);
else
return max(lcs(X, Y, m, n - 1), lcs(X, Y, thousand - i, n));
}
static int max( int a, int b)
{
return (a > b)? a : b;
}
public static void Master()
{
String s1 = "AGGTAB" ;
String s2 = "GXTXAYB" ;
char [] X=s1.ToCharArray();
char [] Y=s2.ToCharArray();
int thou = Ten.Length;
int n = Y.Length;
Console.Write( "Length of LCS is" + " "
+lcs( X, Y, 1000, n ) );
}
}
PHP
<?php
function lcs( $10 , $Y , $m , $n )
{
if ( $grand == 0 || $due north == 0)
return 0;
else if ( $Ten [ $m - one] == $Y [ $north - 1])
return ane + lcs( $10 , $Y ,
$k - ane, $n - 1);
else
render max(lcs( $X , $Y , $thou , $n - 1),
lcs( $X , $Y , $one thousand - 1, $due north ));
}
$X = "AGGTAB" ;
$Y = "GXTXAYB" ;
echo "Length of LCS is " ;
repeat lcs( $X , $Y , strlen ( $X ),
strlen ( $Y ));
?>
Javascript
<script>
function lcs( X, Y , m , n )
{
if (m == 0 || n == 0)
return 0;
if (10[m-1] == Y[north-i])
render 1 + lcs(X, Y, grand-i, n-1);
else
render max(lcs(X, Y, one thousand, due north-1), lcs(Ten, Y, m-i, n));
}
function max(a , b)
{
return (a > b)? a : b;
}
var s1 = "AGGTAB" ;
var s2 = "GXTXAYB" ;
var X=s1;
var Y=s2;
var m = 10.length;
var n = Y.length;
document.write( "Length of LCS is" + " " +
lcs( X, Y, m, n ) );
</script>
Output:
Length of LCS is iv
Time complication of the above naive recursive approach is O(2^n) in worst instance and worst case happens when all characters of X and Y mismatch i.e., length of LCS is 0.
Considering the above implementation, following is a partial recursion tree for input strings "AXYT" and "AYZX"
lcs("AXYT", "AYZX") / lcs("AXY", "AYZX") lcs("AXYT", "AYZ") / / lcs("AX", "AYZX") lcs("AXY", "AYZ") lcs("AXY", "AYZ") lcs("AXYT", "AY") In the above partial recursion tree, lcs("AXY", "AYZ") is beingness solved twice. If we describe the consummate recursion tree, then nosotros can run into that at that place are many subproblems which are solved again and again. So this trouble has Overlapping Substructure property and recomputation of same subproblems can exist avoided by either using Memoization or Tabulation. Following is a tabulated implementation for the LCS problem.
Python3
def lcs(s1 , s2):
m, n = len (s1), len (s2)
prev, cur = [ 0 ] * (northward + ane ), [ 0 ] * (n + 1 )
for i in range ( i , m + 1 ):
for j in range ( 1 , northward + 1 ):
if s1[i - one ] = = s2[j - 1 ]:
cur[j] = i + prev[j - 1 ]
else :
if cur[j - 1 ] > prev[j]:
cur[j] = cur[j - one ]
else :
cur[j] = prev[j]
cur, prev = prev, cur
render prev[n]
s1 = "AGGTAB"
s2 = "GXTXAYB"
impress ( "Length of LCS is " , lcs(s1, s2))
C
#include<bits/stdc++.h>
int max( int a, int b);
int lcs( char *X, char *Y, int m, int n )
{
int L[thou+1][n+1];
int i, j;
for (i=0; i<=grand; i++)
{
for (j=0; j<=due north; j++)
{
if (i == 0 || j == 0)
L[i][j] = 0;
else if (10[i-i] == Y[j-ane])
L[i][j] = L[i-1][j-1] + 1;
else
L[i][j] = max(50[i-i][j], Fifty[i][j-ane]);
}
}
return L[yard][n];
}
int max( int a, int b)
{
render (a > b)? a : b;
}
int main()
{
char X[] = "AGGTAB" ;
char Y[] = "GXTXAYB" ;
int thousand = strlen (X);
int n = strlen (Y);
printf ( "Length of LCS is %d" , lcs( X, Y, m, n ) );
render 0;
}
Java
public class LongestCommonSubsequence
{
int lcs( char [] X, char [] Y, int m, int north )
{
int L[][] = new int [1000+ 1 ][north+ ane ];
for ( int i= 0 ; i<=m; i++)
{
for ( int j= 0 ; j<=n; j++)
{
if (i == 0 || j == 0 )
50[i][j] = 0 ;
else if (X[i- 1 ] == Y[j- 1 ])
50[i][j] = 50[i- 1 ][j- 1 ] + 1 ;
else
L[i][j] = max(L[i- ane ][j], L[i][j- 1 ]);
}
}
render 50[m][n];
}
int max( int a, int b)
{
return (a > b)? a : b;
}
public static void main(Cord[] args)
{
LongestCommonSubsequence lcs = new LongestCommonSubsequence();
Cord s1 = "AGGTAB" ;
String s2 = "GXTXAYB" ;
char [] X=s1.toCharArray();
char [] Y=s2.toCharArray();
int m = 10.length;
int north = Y.length;
System.out.println( "Length of LCS is" + " " +
lcs.lcs( X, Y, m, northward ) );
}
}
Python3
def lcs(10 , Y):
chiliad = len (10)
n = len (Y)
L = [[ None ] * (due north + 1 ) for i in range (m + 1 )]
for i in range (m + i ):
for j in range (north + 1 ):
if i = = 0 or j = = 0 :
Fifty[i][j] = 0
elif Ten[i - ane ] = = Y[j - 1 ]:
Fifty[i][j] = L[i - 1 ][j - one ] + 1
else :
L[i][j] = max (50[i - i ][j] , L[i][j - 1 ])
render L[1000][northward]
10 = "AGGTAB"
Y = "GXTXAYB"
print ( "Length of LCS is " , lcs(X, Y) )
C#
using Arrangement;
class GFG
{
static int lcs( char [] X, char [] Y, int g, int northward )
{
int [,]L = new int [m+ane,north+ane];
for ( int i = 0; i <= m; i++)
{
for ( int j = 0; j <= north; j++)
{
if (i == 0 || j == 0)
Fifty[i, j] = 0;
else if (X[i - 1] == Y[j - one])
L[i, j] = L[i - i, j - 1] + 1;
else
L[i, j] = max(Fifty[i - 1, j], L[i, j - 1]);
}
}
return L[m, n];
}
static int max( int a, int b)
{
return (a > b)? a : b;
}
public static void Main()
{
String s1 = "AGGTAB" ;
String s2 = "GXTXAYB" ;
char [] X=s1.ToCharArray();
char [] Y=s2.ToCharArray();
int m = X.Length;
int n = Y.Length;
Console.Write( "Length of LCS is" + " " +lcs( X, Y, m, n ) );
}
}
PHP
<?php
function lcs( $X , $Y )
{
$m = strlen ( $X );
$due north = strlen ( $Y ) ;
for ( $i = 0; $i <= $thousand ; $i ++)
{
for ( $j = 0; $j <= $north ; $j ++)
{
if ( $i == 0 || $j == 0)
$L [ $i ][ $j ] = 0;
else if ( $X [ $i - 1] == $Y [ $j - 1])
$50 [ $i ][ $j ] = $L [ $i - 1][ $j - 1] + i;
else
$50 [ $i ][ $j ] = max( $L [ $i - 1][ $j ],
$L [ $i ][ $j - i]);
}
}
return $L [ $thousand ][ $n ];
}
$Ten = "AGGTAB" ;
$Y = "GXTXAYB" ;
echo "Length of LCS is " ;
echo lcs( $X , $Y );
?>
Javascript
<script>
function max(a, b)
{
if (a > b)
return a;
else
return b;
}
function lcs(X, Y, m, n)
{
var L = new Array(m + 1);
for ( var i = 0; i < L.length; i++)
{
50[i] = new Assortment(due north + i);
}
var i, j;
for (i = 0; i <= grand; i++)
{
for (j = 0; j <= n; j++)
{
if (i == 0 || j == 0)
Fifty[i][j] = 0;
else if (X[i - i] == Y[j - 1])
L[i][j] = L[i - 1][j - 1] + i;
else
L[i][j] = max(L[i - 1][j], L[i][j - 1]);
}
}
return L[m][north];
}
var x = "AGGTAB" ;
var y = "GXTXAYB" ;
var grand = x.length;
var due north = y.length;
document.write( "Length of LCS is " + lcs(10, y, yard, n));
</script>
Output:
Length of LCS is 4
Time Complication of the above implementation is O(mn) which is much meliorate than the worst-case time complication of Naive Recursive implementation.
The above algorithm/code returns simply length of LCS. Please see the following post for printing the LCS.
Press Longest Common Subsequence
Y'all tin can as well bank check the space optimized version of LCS at
Infinite Optimized Solution of LCS
Delight write comments if y'all find anything wrong, or you want to share more than data about the topic discussed above.
Contempo Manufactures based on LCS!
References:
http://world wide web.youtube.com/watch?5=V5hZoJ6uK-s
http://www.algorithmist.com/index.php/Longest_Common_Subsequence
http://www.ics.uci.edu/~eppstein/161/960229.html
http://en.wikipedia.org/wiki/Longest_common_subsequence_problem
How to Do Lcs When You Dont Know How Many Strings Are in a File C++
Source: https://www.geeksforgeeks.org/longest-common-subsequence-dp-4/
0 Response to "How to Do Lcs When You Dont Know How Many Strings Are in a File C++"
Post a Comment